Adding all digits in a sequence of length L: What is the distrubution of these sums?
GENERAL CONSIDERATIONS / EXPECTED VALUES
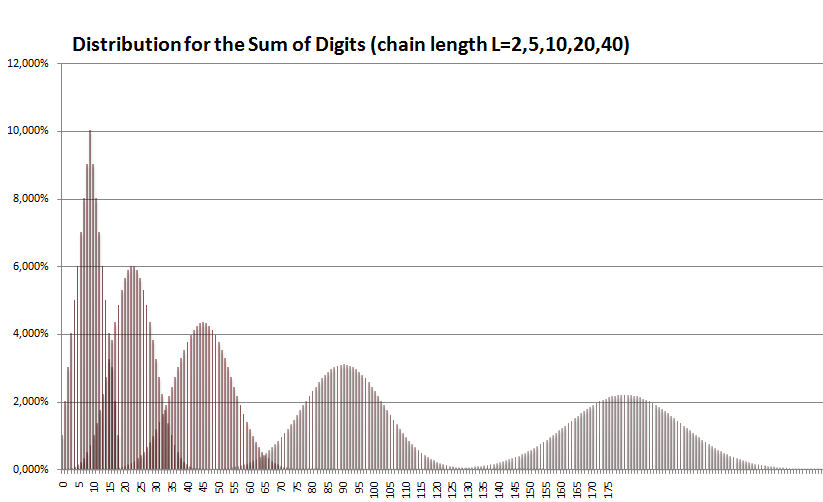
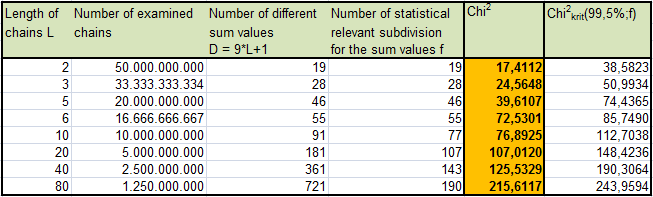
The idea of this test is to divide data into substrings of length L, building the sum of digits of each substring and calculating the Chi2-value for the sum's distribution.
Here is an example for the Pi digits with L=5.
First sequence 14159 -> SUM = 20
Second sequence 26535 -> SUM = 21
Third sequence 89793 -> SUM = 36
For a single digit (L=1) the sum is equal to the digits value and thus we have a probability of 1/10 for any sum of digits from 0 to 9. Let w(L,S) be the probability that a chain of length L has a sum of digits equal to S, then w(1,y)=1/10 with y=0,1,..,9 and w(1,y)=0 when y>9.
Any further distribution can be calculated recursively:
w(L,y) = w(L-1,y) + 1/10 * sum (for all i=0..y) w(L-1,y-i)
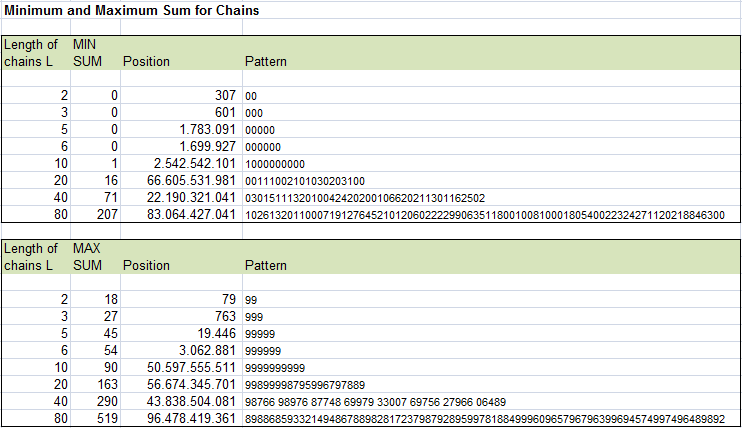
For any L the sum of digits is located between S=0 (all digits=0) and S=9*L (all digits=9). When going to longer and longer chains the min and max sums became extremely improbable because the likelihood for a single digit long run falls like 10-L.
RESULTS
Additional note 2025-11-01
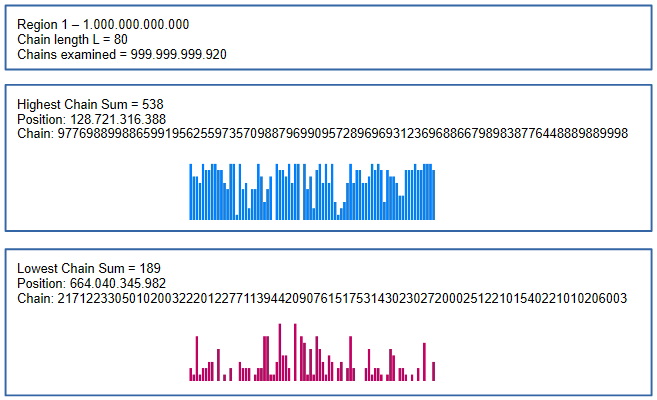
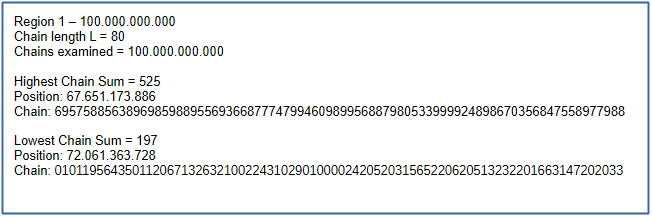
In our investigation, we moved the starting point of the chains forward by L in each case.
To analyze all chains in the area, we move forward by 1 each time.
This is how we find the highest and lowest chain sums in the range of 1-100.000.000.000
Additional note 2025-11-10
Extended search up to 10^12