Sequences that name there own position

GENERAL CONSIDERATIONS / EXPECTED VALUES

It can be very interesting to explore the self referential qualities of a digit sequence. One special kind of that is a correspondence between a subsequence and its absolute position in the whole sequence.
If we find the sequence "klm...nop" exactly at position (klm...nop) we call this a CUCKOO POSITION (German: Kuckuckszahl).

Another definition of CUCKOO could be:
SEQUENCE = POSITION of SEQUENCE

The position predicts the following sequence like the couckoo bird shouts its own name.

The first Cuckoo Position K₁ is not hard to find because Pi starts with "1" at position 1 (after the decimal point):   14159265...

But where comes the next Couckoo Position and how many of them will be found amongst our 100 billion digits?

RESULTS: All Cuckoo-Position up to 100.000.000.000

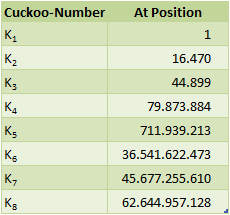
Verified 2017/11/03 when analyzing 10¹² digits:

K₉ = 656.430.109.694

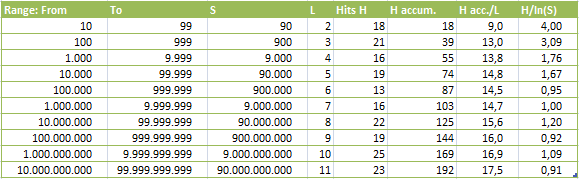
RESULTS: Hits per Range

We can extend our view to NEAR CUCKOO POSITIONS which are not exact hits but pretty close to it.

This unfolds a basic statistical behaviour:

If you increase the data tenfold, you generally get one more cuckoo hit.

S = Sequences proofed; L = Length of Sequences
H = Hits (where ABS(Pos.-Value)<10)